Hi!
Ik heb morgen een herkansing, en de onderstaande vraag staat op veel punten, maar ik weet niet hoe ik hem juist kan oplossen. Kunnen de wiskunde-slimmeriken onder jullie me helpen?
De vraag:
Aan de voet van een steile weg zie je op de top van de heuvel aan het eind van de weg een watertoren staan.
Het gemiddelde stijgingspercentage van de weg is 15 % , dat betekent dat de tangens van de hellingshoek 0,15 bedraagt. Ten opzichte van de helling zie je de top van de watertoren onder een hoek van 1,5° . Van het kijkpunt tot de voet van de toren is weg in vogelvlucht 450 meter lang.
Maak een schets van de situatie en bereken de hoogte van de watertoren.
Ik heb ook een schets gemaakt:
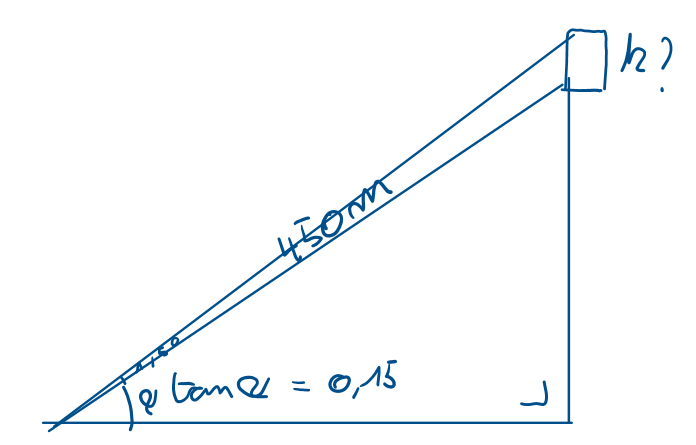
Alvast bedankt voor jullie hulp!!
Rode druif





